Shor’s algorithm is a quantum algorithm that can be used to solve certain mathematical problems much faster than classical algorithms. It is especially important in applications of quantum information science and the development of quantum computing.
It was developed in 1994 by American mathematician Peter Shor, and has been shown to be effective for problems such as integer factorization and the discrete logarithm problem.

Peter Shor
One of the most exciting potential applications of Shor’s algorithm is its ability to break modern cryptography, which is currently protected by quantum-resistant algorithms.
However, the full potential of Shor’s algorithm has yet to be explored, and it is possible that there are other applications that we have yet to discover.
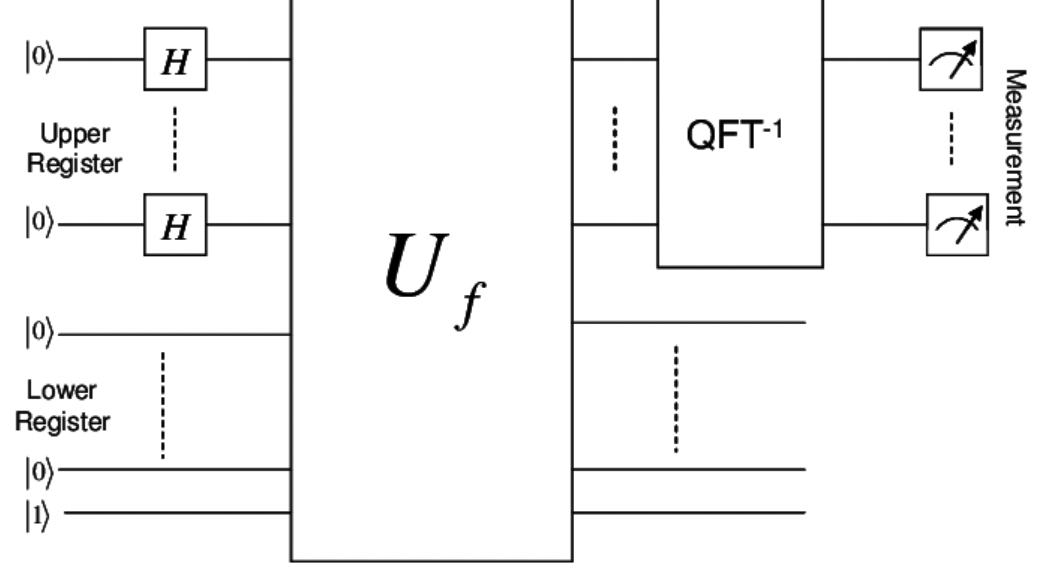
Shor’s algorithm can be divided into two parts:
1) The first part of the algorithm turns the factoring problem into the problem of finding the period of a function and may be implemented classically.
2) The second part finds the period using the quantum Fourier transform and is responsible for the quantum speedup.
The efficiency of Shor’s algorithm is because of the efficiency of the quantum Fourier transform, and modular exponentiation via repeated squarings.
If a quantum computer with an adequate number of qubits could operate without being affected by quantum noise and other quantum-decoherence phenomena, Shor’s algorithm can help break public-key cryptography schemes, such as:
- The RSA scheme
- The Finite Field Diffie-Hellman key exchange
- The Elliptic Curve Diffie-Hellman key exchange
Public-key cryptography
Public-key cryptography is a type of encryption that uses two keys – a public key and a private key.
The public key can be shared with anyone, while the private key must remain secret.
Public-key cryptography is currently considered to be quantum-safe, but could be vulnerable to Shor’s algorithm if a quantum computer with enough qubits became available.
RSA scheme
RSA scheme is a cryptosystem that uses two large prime numbers, along with some additional mathematical operations, to encrypt and decrypt messages.
It is currently considered to be quantum-safe, meaning that it is secure against Shor’s algorithm.
However, if a quantum computer were to become available that could break RSA, then all messages encrypted using this scheme would be vulnerable.
Finite Field Diffie-Hellman key exchange
The Finite Field Diffie-Hellman key exchange is a method of securely exchanging keys over an insecure channel.
It is currently considered to be quantum-safe, but could be vulnerable to Shor’s algorithm if a quantum computer with enough qubits became available.
Elliptic Curve Diffie-Hellman key exchange
The Elliptic Curve Diffie-Hellman key exchange is a method of securely exchanging keys over an insecure channel.
It is currently considered to be quantum-safe, but also potentially vulnerable to Shor’s algorithm if a quantum computer with enough qubits became available.
Related algorithms: GEECM and Grover’s
GEECM and Grover’s algorithm are similar to Shor’s algorithm.
GEECM (Green’s exponential algorithm for integer factorization) is a quantum algorithm that can be used to find the prime factors of an integer.
Grover’s algorithm is a quantum algorithm that can be used to search an unsorted list of items for a specific item.
Both GEECM and Grover’s algorithm are considered to be sub-optimal, meaning that they are not as efficient as Shor’s algorithm.
However, both GEECM and Grover’s algorithm are relatively easy to implement on a quantum computer, which could make them useful in practice.


![Backwards 3: How to Type "Ɛ" [EASY]](https://softwareblade.com/wp-content/uploads/2022/02/Screen-Shot-2022-02-19-at-9.03.25-PM-150x150.png)